指数平滑移動平均は、直近の価格に比重を置いた移動平均で、EMA(Exponential Moving Average)とも言われています。
また、テクニカル分析指標の一つである「MACD」でも、この指数平滑移動平均を利用しています。
本記事では、指数平滑移動平均線の特徴や計算式と、単純移動平均線との違いについて解説します。
単純移動平均と指数平滑移動平均の違いは?
まず初めに、指数平滑移動平均を詳しく解説する前に、単純移動平均(一般的な移動平均)との違いについて説明しましょう。
それぞれの移動平均線を実際のチャートで比較してみると以下のようになります。
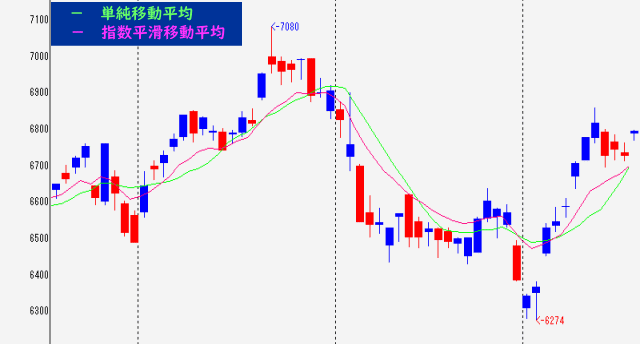
2つの移動平均線は、どちらも10日間の移動平均です。比較してみると単純移動平均よりも指数平滑移動平均の方が株価チャートに近い動きになっていることがわかります。
では、この2つの移動平均の違いはどこにあるのでしょうか?単純移動平均は、その名の通り「全期間の値を単純に平均化」した移動平均です。
対して、指数平滑平均は一言で表現すると「過去よりも直近の値を重視した移動平均」ということです。
単純移動平均は全ての終値が同じ価値
例えば、期間が10日間の単純移動平均線では、9日前の株価も当日の株価も同じ価値を持つことになります。
数式では「10日の単純移動平均=(9日前の終値+8日前の終値+‥+当日の終値)÷10日」ですから、何日前かに関わらず、その株価の終値の価値は平等だからです。

指数平滑移動平均は直近の終値の方が価値が高い
しかし、指数平滑移動平均線は、当日に近い株価ほど価値が大きくなるように計算された移動平均になります。

では、その計算式はどうなっているのでしょうか?
指数平滑移動平均の計算式
計算式は以下のようになります。
- n日間の指数平滑移動平均(EMA)
- 1日目=n日の終値の平均(初日のみ単純移動平均)
- 2日目以降=前日のEMA+α×{当日終値-前日のEMA}
- ※α(平滑化定数)=2÷(n+1)
指数平滑移動平均の計算式の具体例
上の計算式に当てはめて、5日間の指数平滑移動平均を計算するとすれば、導くために必要な数値は以下のようになります。
- 1日目の5日単純移動平均(SMA)
- 2日目のEMA=初日の5日SMA+(当日の終値ー初日の5日SMA)×1/3
- 3日目のEMA=2日目のEMA+(当日の終値ー2日目のEMA)×1/3
- 4日目のEMA=3日目のEMA+(当日の終値ー3日目のEMA)×1/3
- 5日目のEMA=4日目のEMA+(当日の終値ー4日目のEMA)×1/3
平滑移動平均線のポイントは「初日の単純移動平均(SMA)」と「平滑定数」です。
平滑移動平均線の初日は単純移動平均線(SMA)
指数平滑移動平均を算出する初日に関しては、単純移動平均が用いられます。
平滑化定数
「平滑化定数」は直近の株価を重視するために用いる定数です。
計算式は「2回÷(n+1)日」となり、5日間の平滑移動平均線では平滑化定数は1/3になります。
平滑移動平均線は当日の値を重視
算出式からわかることは「指数平滑移動平均線は前日までの終値を継ぎ足していくイメージ」です。
飲食店などにある秘伝のタレと同じく、指数平滑移動平均線は継ぎ足しによって作られた移動平均線ということです。
古いタレの成分はどんどん希釈化されて、新しく足されたタレの方がずっと成分が多くなります。
指数平滑移動平均線も同じで、過去の株価の終値はどんどん希釈化されていき、新しく加えられた株価の終値による比重がどんどん大きくなっていくという事です。
指数平滑移動平均の利用方法
指数平滑移動平均のメリットは「単純移動平均の遅効性をカバーしている」という点です。
そのため、ゴールデンクロスやデッドクロスによる売買サインは、単純移動平均線より早く出現するので、売買タイミングは計りやすくなるでしょう。
しかし、一方で直近の株価の影響が強く、株価が大きくぶれた時には、それらの売買サインがフェイクになりやすいという特徴もあります。
MACDは指数平滑移動平均を利用したテクニカル分析
指数平滑移動平均は、MACDと言われるテクニカル分析に用いられています。
MACDは「短期のEMA-短期EMAのライン」と「MACDラインのSMA(単純移動平均)」の2本のラインのゴールデンクロスとデッドクロスから売買判断をするテクニカル分析です。
MACDは、単純移動平均線による遅効性を補うために、指数平滑移動平均を用いることで、株価チャートに連動する売買判断を実現するために作られたテクニカル分析です。
ですから、MACDを使えば、指数平滑移動平均を利用したテクニカル分析を行うことができます。



